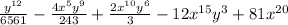Question

I need help with this practice problem It asks to answer (a) & (b) Please put (a) & (b) separately so I know which one is which

Answer 1

The Binomial Theorem

It describes the algebraic expansion of powers of a binomial.

The general formula for the expansion of the binomial is:

`(a+b)^n=\sum ^(k=n)_(k=0)\binom{n}{k}a^kb^(n-k)`

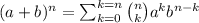
Given the expression:

`\mleft(3x^5-(1)/(9)y^3\mright)^4`

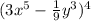
This corresponds to the formula written above for the values:

`a=3x^5,b=-(1)/(9)y^3,n=4`

(a) The expression can be written in summation form as:

`(3x^5-(1)/(9)y^3)^4=\sum ^(k=4)_(k=0)\binom{4}{k}(3x^5)^k\mleft(-(1)/(9)y^3\mright)^(4-k)`

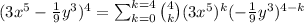
(b) It's required to write the full expansion. We expand the summation as follows (the left part will be omitted for limitations of space):

`\begin{gathered} \binom{4}{0}(3x^5)^0\mleft(-(1)/(9)y^3\mright)^4+\binom{4}{1}(3x^5)^1(-(1)/(9)y^3)^3+\binom{4}{2}(3x^5)^2(-(1)/(9)y^3)^2+ \\ +\binom{4}{3}(3x^5)^3(-(1)/(9)y^3)^1+\binom{4}{4}(3x^5)^4(-(1)/(9)y^3)^0 \end{gathered}`

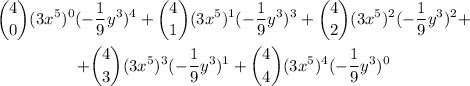
Operating:

`\begin{gathered} 1\cdot(1)^{}((1)/(6561)y^(12))^{}+4(3x^5)(-(1)/(729)y^9)+6(9x^(10))((1)/(81)y^6)+ \\ +4(27x^(15))(-(1)/(9)y^3)+1\cdot(81x^(20))(1) \end{gathered}`

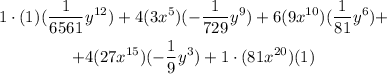
Simplifying:

`(y^(12))/(6561)^{}-(4x^5y^9)/(243)+(2x^(10)y^6)/(3)-12x^(15)y^3+81x^(20)`