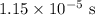Question

a radioactive substance, fermium-253, has a half-life of three days. how long will it take for this isotope to decay to one-eighth of its original amount?

Answer 1

Radioactive decay is characterized by the formula

`N=((1)/(2))^{(t)/(t_h)}N_0`

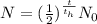
Where N is the amount of the element remaining,

`N_0\text{ is initial amount of the element}`

t is the time taken to reduce the amount of the element to N and th is the half life of the element

In this case

`N=(N_0)/(8)`

And

`th=3days=3*24*60*60=2.6*10^5\text{ s}`

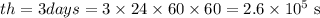
We need to find t

So we substitute the known values in the above equation

`(N_0)/(8)=N_0*((1)/(2))^{(t)/(2.6*10^5)}`

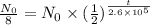
Which is

`(1)/(8)=((1)/(2))^{(t)/(2.6*10^5)}`

Taking the log on both sides,

`\log ((1)/(8))=-\log (8)=(t)/(2.6*10^5)\log ((1)/(2))`

Simplifying,

`-0.9=(-0.3* t)/(2.6*10^5)`

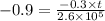
On rearranging and further simplifying we get,

`t=1.15*10^(-5)\text{ s}`

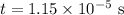
Thus the time taken for fermium 253 to reduce to one-eight of its initial amount is

`1.15*10^(-5)\text{ s}`