Question

RS2. Given: ZP ZQ andProve: PR=QRSupply the missing reason in Statement 1 of the proof of the the Converse of the Isosceles Triangle Theorem.Begin with isosceles APRQ with ZP ZQ. Construct RS, a bisector of ZPRQ.bisects ZPQR.R

Answer 1

We are given the following triangle:

We are given that:

`\angle P=\angle Q`

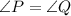
Since RS is a bisector this means that:

`\angle PRS=\angle SRQ`

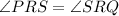
Also, since S is a midpoint of PQ:

`PS=SQ`

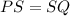
By the reflexive property we have:

`RS=RS`

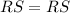
Since we have two pairs of congruent angles this means that:

`\angle PSR=\angle QSR`

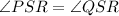
Therefore, by SAS theorem of congruency:

`\Delta PSR\cong\Delta QSR`

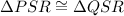
Since the triangles are congruent this means that all of its sides are congruent too, therefore:

`PR=QR`

And thus we have concluded the proof.