Question

A ladder is leannig againts a wall. The distance of the bottom of the ladder from the wall is 4 feet less than the length of the ladder. The top of the ladder from the floor is 2 feet less than the length of the ladder. Determine the length of the ladder,

Answer 1

In a diagram,

Where l is the length of the ladder.

Therefore, using the Pythagorean theorem,

`l^2=(l-2)^2+(l-4)^2`

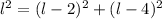
Solving for l,

`\begin{gathered} \Rightarrow l^2=l^2-4l+4+l^2-8l+16 \\ \Rightarrow l^2-12l+20=0 \end{gathered}`

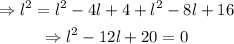
Solve using the quadratic formula,

`\begin{gathered} \Rightarrow l=(12\pm√(144-4*20))/(2) \\ \Rightarrow l=(12\pm√(64))/(2) \\ \Rightarrow l=(12\pm8)/(2) \\ \Rightarrow l=2,10 \end{gathered}`

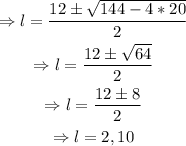
However, notice that if l=2, l-4 would be negative which is impossible as it is a length.

Therefore, the only valid answer is l=10.

The answer is that the length of the ladder is 10ft