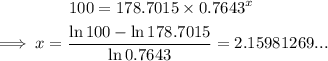Question

1. Make a scatter plot of the table provided in the image.B. Write a linear/exponential equation that models this tableC. Explain what the slope/multiplier means in the context of this problemD. Use your models to predict where there will be 100 new cases

Answer 1

Part A:

A scatter plot is a set of points plotted on a horizontal and vertical axes. If we use the left column as the 'horizontal' variable and the right column as the 'vertical' variable, we have the following scatterplot:

Part B:

Regression models describe the relationship between variables by fitting a line to the observed data. Linear regression models use a straight line. A line equation has the form:

`y=mx+b`

where m represents the slope and b the y-intercept.

Using the least square method to determinate those coefficients, the line regression model equation for our dataset is:

`y=-24.14x+161.2`

For this line we have the following graph:

Exponential regression models use an exponential curve. A exponential equation has the form:

`y=a(b)^x`

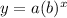
Where a represents the initial value and b represents the growth/decay rate.

Using the exponential regression model, we have the following equation:

`y=178.7015\cdot0.7643^x`

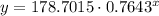
This equation has the following graph:

Part C:

The slope/multiplier represents the rate the graph decreases. On the context of the problem, the rate that new cases appear.

Part D:

For each model, we just have to solve the following equation:

`y=100`

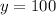
Solving for the linear model, we have:

`\begin{gathered} 100=-24.14x+161.2 \\ \implies x=(100-161.2)/(-24.14)=2.53521127... \end{gathered}`

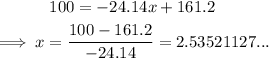
Solving for the exponential model, we have:

`\begin{gathered} 100=178.7015*0.7643^x \\ \implies x=(\ln100-\ln178.7015)/(\ln0.7643)=2.15981269... \end{gathered}`