ANSWER
The material is Crown Glass.
Step-by-step explanation
We have the following situation,
By Snell's Law,
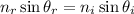
In this problem, we have:
• The refractive index of air, ni = 1.003
,
• The angle of incidence, θi = 60°
,
• The angle of refraction, θr = 34.85°
And we have to find the material of the glass, which can be found using the table and finding its index of refraction, nr. To do so, divide both sides of the equation above by sin(θr),
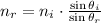
Replace the known values and solve,
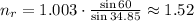
As we can see in the given table, the material with a refractive index of 1.52 is crown glass,