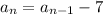Answer:
The recursive formula is;
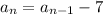
Step-by-step explanation:
We want to find the recursive formula for the given sequence;
The recursive can be in the form;
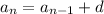
where d is the common difference.
Let us find the common difference for the given sequence;
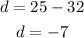
So, the recursive formula can be derived by substituting the value of d into the equation above;
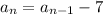
Therefore, the recursive formula is;