We have that the formula for Continuous Compounding Interest is given by the formula:
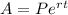
We have from the question, the following information:
1. We need the approximate balance after t = 1, t = 5, t = 20 years.
2. P = $12,000.
3. r = 3.5 ---> r = 3.5/100 = 0.035.
4. e is the value for the e = 2.7172...
Then, we have:
a. Approximated Balance after t = 1. Then, we have:
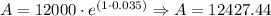
b. Approximated Balance after t = 5. In this case, we can proceed in a similar way:
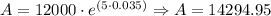
c. Approximated Balance after 20 years:
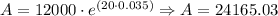
Therefore, the approximated balance in the account after:
One year ---> A = $12427.44.
Five years ---> A = $ 14294.95
Twenty years ---> A = $ 24165.03
By the way, APR is the Annualized Percentage Rate.