Question

A triangle has a perimeter of 25 inches. The medium side is 7 more than the short side, and the longest side is 4times the length of the shortest side. Find the shortest side.The shortest side isinches.

Answer 1

3 inches

Step-by-step explanation

Let 'x' be the shortest side of this triangle. We know that the medium side is 7 more than the short side, so this is (x + 7). Also, the longest side is 4 times the short side, so this is 4x.

Knowing that the perimeter - which is the sum of all three sides, is 25 inches, we can write an equation for x,

`x+(x+7)+4x=25`

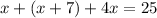
Add like terms,

`\begin{gathered} (x+x+4x)+7=25 \\ \\ 6x+7=25 \end{gathered}`

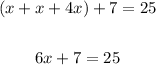
Subtract 7 from both sides,

`\begin{gathered} 6x+7-7=25-7 \\ \\ 6x=18 \end{gathered}`

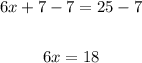
And divide both sides by 6,

`\begin{gathered} (6x)/(6)=(18)/(6) \\ \\ x=3 \end{gathered}`

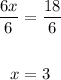
Hence, the shortest side of the triangle is 3 inches long.