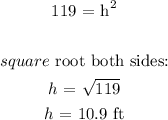Question

How far up the tree is the cat in feet?

Answer 1

Answer:

h = 10.9 ft (nearest tenth)

Step-by-step explanation:

Given:

the longest side (ladder) = 12 ft

Distance from the base of the tree to the foot of the ladder = 5ft

To find:

the distance from the base of the tree to the top of the tree where the cat is located

We will be using Pythagoras theorem as the ladder and tree form a right-angled triangle

Hypotenuse² = opposite² + adjacent²

hyp = 12 ft, opp = h ft, adj = 5 ft

substitute the values:

`\begin{gathered} 12^2\text{ = h}^2+\text{ 5}^2 \\ 144\text{ = h}^2\text{ + 25} \\ \\ substract\text{ 25 from both sides:} \\ 144\text{ - 25 = h}^2 \end{gathered}`
`\begin{gathered} 119\text{ = h}^2 \\ \\ square\text{ root both sides:} \\ h\text{ = }√(119) \\ h\text{ = 10.9 ft} \end{gathered}`