As one can see, this is an Isosceles triangle; therefore, the angles between the legs and the base are congruent. Since JL and JK are congruent, those are the legs of the triangle and

Furthermore, the sum of the inner angles of a triangle is equal to 180°; thus
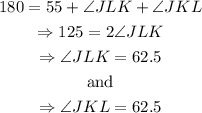
The answer is that angles