Question

The sum of two numbers is 24. The second number is 3 times the first number. Write a system of equations and find the two numbers.

Answer 1

Let x and y be such numbers. Since their sum is 24, then:

`x+y=24`

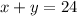
Since the second number is 3 times the first number, then:

`y=3x`

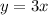
Solve the system of equations using the substitution method. Replace y by 3x on the first equation and solve for x:

`\begin{gathered} x+y=24 \\ \Rightarrow x+3x=24 \\ \Rightarrow4x=24 \\ \Rightarrow x=(24)/(4) \\ \therefore x=6 \end{gathered}`

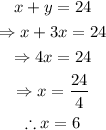
Substitute x=6 in the expression for y to find its value:

`\begin{gathered} y=3x \\ \Rightarrow y=3(6) \\ \therefore y=18 \end{gathered}`

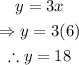
Therefore, those numbers are 6 and 18 (notice that 6+18 = 24 and 18 is three times 6)-