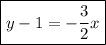Question

Write an equation in point-slope form of the line that passes through the point (0, 1) and has a slope of −3/2.

Answer 1

`\displaystyle y-1=-(3)/(2)x`

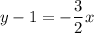
Explanation:

Givens

We are given that the equation we wish to determine has a slope of:

`\displaystyle -(3)/(2)`

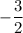
This is also referred to as m.

We are also told that the equation will pass through the point:

`(0, 1)`

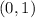
This can be written as:

• x₁ = 0
• y₁ = 1

The final equation must be written in the point-slope form:

`y-y_1=m(x-x_1)`

Solve

First, substitute the slope as m into the formula:

`\displaystyle y-y_1=-(3)/(2)(x-x_1)`

Then, substitute x₁ and y₁ into the formula:

`\displaystyle y-1=-(3)/(2)(x-0)`

Finally, simplify by removing the redundant constant:

`\displaystyle y-1=-(3)/(2)x`

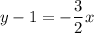
Therefore, the final equation in point-slope form is:

`\displaystyle \boxed{y-1=-(3)/(2)x}`