Question

Perform the indicated operation to determine if the givensimplification is correct. If it is correct, select TRUE. If it is notcorrect, select FALSE.(x+7)/(x² + 12x + 35) : (x+3)/(x+5) = 1/(x+3)

Answer 1

In order to simplify this expression, first let's put the denominator of the first fraction in the factored form:

`ax^2+bx+c=a(x-x_1)(x-x_2)`

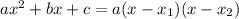
To do so, let's find the zeros of the polynomial using the quadratic formula:

`\begin{gathered} x^2+12x+35=0 \\ a=1,b=12,c=35 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_1=\frac{-12+\sqrt[]{144-140}}{2}=(-12+2)/(2)=-5 \\ x_2=(-12-2)/(2)=-7 \end{gathered}`

So we have:

`x^2+12x+35=(x+5)(x+7)`

Now, let's simplify the expression by inverting the division (turning it into a product) and canceling the like terms:

`\begin{gathered} ((x+7))/((x+5)(x+7))\colon((x+3))/((x+5)) \\ =(1)/(x+5)\cdot(x+5)/(x+3) \\ =(1)/(x+3) \end{gathered}`

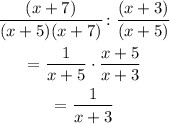
The right side of the expression is correct, therefore the answer is TRUE.