Question

I need help with the radical I don’t know how to solve it because I don’t know how to use the radical

Answer 1

We need to draw a right triangle and label the right angle and theta. Also label the legs.

The hypotenuse measures 3*square root(3).

The opposite leg measures 3.

To find the adjacent leg we can apply the Pythagorean Theorem:

`h^2=a^2+b^2`

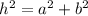
Where h is the hypotenuse, a and b are the legs of the triangle.

We can replace h and a with the known values, and solve for b:

`\begin{gathered} b^2=h^2-a^2 \\ b^2=(3\sqrt[]{3})^2-3^2 \\ b^2=3^2\cdot(\sqrt[]{3})^2-3^2 \\ b^2=9\cdot3-9 \\ b^2=27-9 \\ b^2=18 \\ \sqrt[]{b^2}=\sqrt[]{18} \\ b=\sqrt[]{9*2} \\ b=\sqrt[]{9}*\sqrt[]{2} \\ b=3\sqrt[]{2} \end{gathered}`

Then, the adjacent leg measures 3*square root(2).

Now, we need to find the 6 trigonometric functions:

Start with the sine function:

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \sin \theta=\frac{3}{3\sqrt[]{3}} \\ We\text{ can simplify 3/3=1} \\ \sin \theta=\frac{1}{\sqrt[]{3}} \end{gathered}`

Cosine:

`\begin{gathered} \cos \theta=(adjacent)/(hypotenuse) \\ \cos \theta=\frac{3\sqrt[]{2}}{3\sqrt[]{3}} \\ \text{Simplify 3/3=1} \\ \cos \theta=\frac{\sqrt[]{2}}{\sqrt[]{3}} \\ \text{Apply the quotient property of square roots} \\ \cos \theta=\sqrt[]{(2)/(3)} \end{gathered}`

Tangent:

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \tan \theta=\frac{3}{3\sqrt[]{2}} \\ \text{Simplify 3/3=1} \\ \tan \theta=\frac{1}{\sqrt[]{2}} \end{gathered}`

Cosecant:

`\begin{gathered} \csc \theta=(hypotenuse)/(opposite) \\ \csc \theta=\frac{3\sqrt[]{3}}{3} \\ Simplify\text{ 3/3=1} \\ \csc \theta=\sqrt[]{3} \end{gathered}`

Secant:

`\begin{gathered} \sec \theta=(hypotenuse)/(adjacent) \\ \sec \theta=\frac{3\sqrt[]{3}}{3\sqrt[]{2}} \\ Simplify\text{ 3/3=1} \\ \sec \theta=\frac{\sqrt[]{3}}{\sqrt[]{2}} \\ \sec \theta=\sqrt[]{(3)/(2)} \end{gathered}`

Cotangent:

`\begin{gathered} \cot \theta=(adjacent)/(opposite) \\ \cot \theta=\frac{3\sqrt[]{2}}{3} \\ \text{Simplify 3/3=1} \\ \cot \theta=\sqrt[]{2} \end{gathered}`