EXPLANATION
The appropiate system of inequalities for the graph is:
(1) x=2 (There is a vertical line)
(2) y=mx + b where m is the slope and b is the y-intercept
The slope is given by the following relationship:
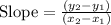
Where (x_1,y_1) and (x_2,y_2) are two ordered pairs from the line.
Considering either one ordered pair, as for instance, (x_1,y_1)=(0,-3) and (x_2,y_2)= (2,0) give us the appropiate slope.
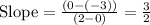
Now, the line equation is as follows:
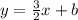
As the y-intercept is b=-3 the equation of the line is:
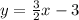
Hence, the system of equations is:
(1) x≥2
(2) y≤ (3/2)x - 3