Question

Here are summary statistics for randonly selected weights of newbor girls: n - 245, x-28.6hg s-7.5hgConstruct a confidence interval estimate of the mean. Use a 90% confidence level, Are these results verydifferent from the confidence interval 27.0 hg

Answer 1

We have to calculate the 90% confidence interval for the mean.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value

(NOTE: although we have a relatively big sample, so it wouldn't be too wrong to approximate the standard deviation of the population with the sample one.. Even though, we will use the Student's t test as usual for unknown population standard deviations).

When σ is not known, s divided by the square root of N is used as an estimate of σM:

`s_M=(s)/(√(N))=(7.5)/(√(245))=(7.5)/(15.652)=0.479`

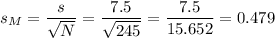
The degrees of freedom for this sample size are:

`df=n-1=245-1=244`

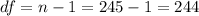
The t-value for a 90% confidence interval and 244 degrees of freedom is t = 1.651.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=1.651\cdot0.479=0.791`

Then, the lower and upper bounds of the confidence interval are:

`\begin{gathered} LL=M-t\cdot s_M=28.6-0.791=27.8 \\ UL=M+t\cdot s_M=28.6+0.791=29.4 \end{gathered}`

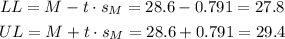
The confidence interval for the population mean is:

`27.8<\mu<29.4`

If we compare this interval with the one calcualted for a smaller sample, we can see that the limits are very similar and both CI contain both sample means.

Answer:

27.8 hg < μ < 29.4 hg.

A. No, because the confidence interval limits are similar.