Question

Two trains leave the station at the same time, one heading west and the other east. The westbound train travels 14 miles per hour slower than the eastbound train. If the two trains are 680 miles apart after 4 hours, what is the rate of the west bound trains? Do not do any rounding

Answer 1

The rate of the west bound trains is 78 miles per hour.

STEP - BY - STEP EXPLANATION

What to find?

The rate of the west bound trains.

Before we proceed to solve the problem, let us take x to represent the rate of the westbound train.

From the given information, we see that x + 14 is the rate of the eastbound train.

We can now set up an equation

distance traveled by eastbound + distance traveled by westbound =distance apart.

where distance apart = 680 miles (from the question).

But we know that;

rate = distance / time

⇒distance = rate x time

From the given question, time =4

So;

Distance traveled by westbound = 4x

Distance traveled by the eastbound =4(x+14)

Hence, we now have:

4(x+14) + 4x = 680

Open the parebthesis.

4x + 56 + 4x = 680

8x + 56 = 680

Subtract 56 from both-side of the equaton.

8x = 680 - 56

8x =624

Divide both-side of the equation by 8.

`\frac{\cancel{8}x}{\cancel{8}}=(624)/(8)`
`x=78`

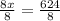
Therefore,the rate of the westbound trains is 78 miles per hour.