Question

Use a sum or different identity to find the exact value:

Answer 1

Given:

The trigonometric expression is given as,

`\sin 105\degree\cos 45\degree-\cos 105\degree\sin 45\degree`

The objective is to find the exact value of the expression.

Step-by-step explanation:

Consider the general formula,

`\sin a\cos b-\cos a\sin b=\sin (a+b)\ldots\text{.}(1)`

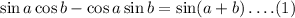
By comparing the given equation with the RHS of equation (1),

`\begin{gathered} a=105\degree \\ b=45\degree \end{gathered}`

To find the value:

On plugging the obtained values of a and b in equation (1),

`\sin 105\degree\cos 45\degree-\cos 105\degree\sin 45\degree=\sin (105-45)`

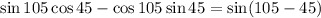
On further solving the above equation,

`\sin 105\degree\cos 45\degree-\cos 105\degree\sin 45\degree=\sin (60)\degree`

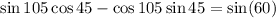
From the trigonometric table,

`\sin 60\degree=\frac{\sqrt[]{3}}{2}`

Hence, the exact value of the expression is √3/2.