The empirical rule
The Empirical Rule states that 99.7% of data observed following a normal distribution lies within 3 standard deviations of the mean. Under this rule, 68% of the data falls within one standard deviation, 95% percent within two standard deviations, and 99.7% within three standard deviations from the mean.
-----------------------------------------------------------------------------------------------------------------
Given,
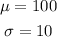
(a)
% of people who have IQ between 70 and 130...
70 and 130 are 3 standard deviations of the mean.
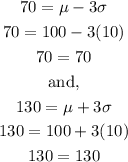
So, that is 99.7% of the people.
Answer - 99.7%
(b)
% of people with IQ less than 90 or greater than 110
"90" and "110" are 1 standard deviation of the mean. So, according to the Empirical Rule, 68% of data fall between 1 standard deviation of the mean.
We want to know what % of data falls outside this 1 standard deviation. That will be:
100 - 68 = 32%
Answer - 32%
(c)
% of people with IQ greate than 120
From the diagram above, we see that the region that is greater than 120 is 2.35%
Answer - 2.35%