Step-by-step explanation:
Given;
We are told that a promissory note of $800 is issued at the rate of 8% ordinary interest and a 180-day term.
Required;
We are required to determine the total payment required to pay off the promissory note.
Step-by-step solution;
For a repayment on a promissory note the interest payable will be calculated by the simple interest method.
That is;
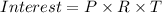
Here, the variables are;
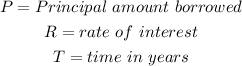
For a 180-day term, the time in years will now be the total number of months divided by 12. This is because the term is not up to a year, and therefore the time will be prorated as a ratio of a complete year (12 months).
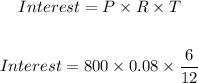
Note here that the 180-day term is the equivalent of 6 months (considering 30 days in a month).
We can now complete the computation of the interest;
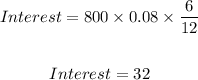
The total repayment will now be the principal amount borrowed plus the interest calculated.
Hence, we have
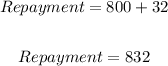
ANSWER:
Option A: $832.00