Question

Help simplify steps of the expression using the properties of rational exponents

Answer 1

Given:

`\sqrt[3]{875x^5y^9}`

Simplify the expression

`\begin{gathered} \sqrt[3]{875x^5y^9} \\ =\sqrt[3]{7*125^{}* x^3* x^2* y^3* y^3* y^3} \\ =\sqrt[3]{7*5^3* x^3* x^2* y^3* y^3* y^3} \end{gathered}`

Simplify further by taking the cube root of the expression

This gives

`\begin{gathered} \sqrt[3]{7*5^3* x^3* x^2* y^3* y^3* y^3} \\ =5* x* y* y* y*\sqrt[3]{7* x^2} \\ =5xy^3\sqrt[3]{7* x^2} \\ =5\cdot x\cdot y^3(7^{(1)/(3)}* x^{(2)/(3)}) \end{gathered}`

The above result can be simplified as

`\begin{gathered} 5\cdot x\cdot y^3(7^{(1)/(3)}* x^{(2)/(3)}) \\ =5^1\cdot7^{(1)/(3)}\cdot x^1\cdot x^{(2)/(3)}\cdot y^3 \end{gathered}`

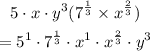
Using the same steps, the given expression can be simplified as shown below

`\begin{gathered} \sqrt[3]{875x^5y^9} \\ =\sqrt[3]{7*125^{}* x^5* y^9} \\ =\sqrt[3]{125*7}*\sqrt[3]{x^5}*\sqrt[3]{y^9} \\ =(125*7)^{(1)/(3)}\cdot x^{(5)/(3)}* y^{(9)/(3)}^{} \end{gathered}`

Solving the given expression completely

`\begin{gathered} \sqrt[3]{875x^5y^9} \\ =(875x^5y^9)^{(1)/(3)} \\ =(125*7)^{(1)/(3)}* x^{(5)/(3)}* y^{(9)/(3)} \\ =125^{(1)/(3)}*7^{(1)/(3)}* x^{((3)/(3)+(2)/(3))}* y^3 \\ =5*7^{(1)/(3)}* x^1* x^{(2)/(3)}* y^3 \\ =5xy^3(7^{(1)/(3)}* x^{(2)/(3)}) \end{gathered}`