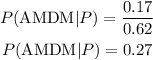Question

A school counts the number of students taking AMDM and find 217 students taking AMDM. They also count the number of students taking Physics and find 249 students takingthe Physics. When they compare the two lists they find 67 student taking AMDM and Physics. What is the probability of a student taking AMDM given they are taking Physics.(Answer in decimal form)

Answer 1

`P(\text{AMDM}|P)=0.27`

Step-by-step explanation

First, let us find the total number of students.

There are 217 students taking AMDM, 249 students taking Physics, and 67 students taking both. The total number of students is:

`\begin{gathered} Total=217+249-67 \\ Total=399 \end{gathered}`

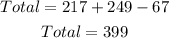
The probability of a student taking AMDM given that they are taking Physics is:

`P(\text{AMDM}|P)=(P(AMDM\cap P))/(P(P))`

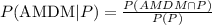
The probability that a student is taking AMDM and Physics is:

`\begin{gathered} P(AMDM\cap P)=\frac{Number\text{ of students taking both}}{Total\text{ number of students}} \\ P(AMDM\cap P)=(67)/(399) \\ P(AMDM\cap P)=0.17 \end{gathered}`

The probability that a student is taking Physics is:

`\begin{gathered} P(P)=\frac{\text{Number of students taking Physics}}{Total\text{ number of students}} \\ P(P)=(249)/(399) \\ P(P)=0.62 \end{gathered}`

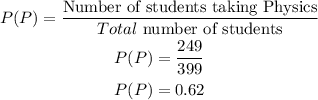
Therefore, the probability of a student taking AMDM given that they are taking Physics is:

`\begin{gathered} P(\text{AMDM}|P)=(0.17)/(0.62) \\ P(\text{AMDM}|P)=0.27 \end{gathered}`