Given:
The life of lightbulbs is distributed normally. The variance of the lifetime is 900 and the mean life time of a bulb is 580 hours.
Required:
Find the probability of a bulb lasting for at most 613 hours
Step-by-step explanation:
The mean lifetime of a bulb = 580 hours
The variance of the lifetime is 900. So, standard deviation will be 30.
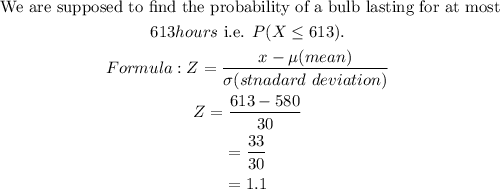
Now from z table
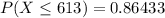
Answer:
The probability of bulb lasting for at most 613 hours is 0.86433