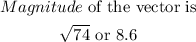Question

What is the magnitude of a vector whose terminal point is at (7,-5)?

Answer 1

Step 1:

The magnitude of a vector is the length of the vector itself.

Given a bi-dimensional vector, the magnitude of the vector is given by:

`\text{v = }√(v_x^2+v_y^2)`

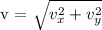
Step 2:

where

Vx is the x-component of the vector

Vy is the y-component of the vector

Step 3:

The vector in the problem is ( 7 , -5 )

Where

`\begin{gathered} v_x\text{ = 7} \\ v_y\text{ = -5} \end{gathered}`

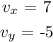
Step 4:

`\begin{gathered} \text{v = }\sqrt{7^2\text{ + \lparen-5\rparen}^2} \\ \text{v = }\sqrt{49\text{ + 25}} \\ \text{v = }√(74) \\ \end{gathered}`

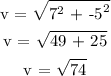
Final answer

`\begin{gathered} Magnitude\text{ of the vector is} \\ √(74)\text{ or 8.6} \end{gathered}`