Question

After heavy winds damaged a house, workers placed a 19-m

brace against its side at a 45° angle. Then, at the same spot
on the ground, they placed a second, longer brace to make a
30° angle with the side of the house. Complete parts a
through b below.
309
19 m
45
X
oring
(a) How long is the longer brace?
nework
The length of the longer brace is Nm.
(Type an integer or a decimal. Round to the nearest tenth as needed.)
(b) How much higher does the longer brace reach than the shorter brace?
The longer brace is m higher than the shorter brace.
(Type an integer or a decimal. Round to the nearest tenth as needed.)
MS
ms

Answer 1

a: 26.9m; b. 9.8m

Explanation:

the 19m brace is the diagonal of a square. You can easily find the side of the quare from the diagonal by deviding it by
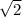`\sqrt2`. At this point we can find how far away the brace is anchored, that is 13.44m. We will need this later.

Now the longer brace. If you stare at the image long enough and try drawing another triangle mirrored horizontally (adding my paint rendition) you see you have created an equilateral triangle, and the horizontal distance from the wall is exactly twice the length of the brace, so 26.88m

Now for the last point, you have a right triangle of which you know two sides. The third is easily solved with the pythagorean theorem, and the top of the longer brace is at an height of 23.27m. That's not what we need, we need the distance from the top of the lower brace, which is at 13.44m from the ground -it's an isosceles triangle since it's a right triangle with an angle of 45° - or half a square, if you prefer - and the difference in height is 9.83m. Now let's round as needed.