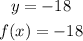Question

Find a linear equation satisfying the followingf(4) = -18 and f(4)= -18f(x) =

Answer 1

You need to find the equation of a function that satisfies:

f(4)= -18

f(4)=-18

If you calculate the slope of the line using the formula:

`m=(y_2-y_1)/(x_2-x_1)`

And the given ordered pairs (4,-18) and (4,-18)

`\begin{gathered} m=((-18)-(-18))/(4-4) \\ m=(-18+18)/(4-4) \\ m=(0)/(0)=0 \end{gathered}`

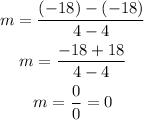
You'll determine that the slope of the line is equal to zero.

Lines with slope zero are horizontal, which means that regardless of the value of x, the value of y will remain the same.

In this case, this value is the y-coordinate of the given ordered pairs y=-18

So the equation of the line, expressed using function notation is:

`\begin{gathered} y=-18 \\ f(x)=-18 \end{gathered}`