Question

1. The number of increase of snails per day in a landfill after monitoring made by the researchers from the Department of Agriculture is described by the function, S(t) = 1000t² + 450t - 1000. Find:a. The average rate of increase of snails from 2 to 3 days.b. The rate of increase of snails after 2 days.

Answer 1

`\begin{gathered} \text{Given} \\ S(t)=1000t^2+450t-1000 \end{gathered}`

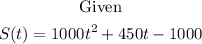
Part A: average rate of increase from 2 to 3 days

Recall the average rate of change formula which is defined as

`\begin{gathered} \text{If }f(x)\text{ is the function, then its average rate of change is} \\ (\Delta y)/(\Delta x)=(f(b)-f(a))/(b-a) \\ \text{where} \\ a\text{ is the lower bound of the interval} \\ b\text{ is the upper bound of the interval} \end{gathered}`

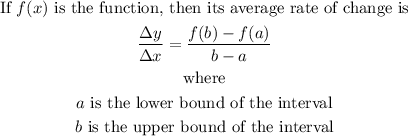
In this instance, the function is S(t) where the lower bound is a = 2, and the upper bound is b = 3.

The average, solve first for S(2) and S(3)

`\begin{gathered} \text{If }t=2 \\ S(t)=1000t^2+450t-1000 \\ S(2)=1000(2)^2+450(2)-1000 \\ S(2)=1000(4)+900-1000 \\ S(2)=4000+900-1000 \\ S(2)=3900 \\ \\ \text{If }t=3 \\ S(t)=1000t^2+450t-1000 \\ S(3)=1000(3)^2+450(3)-1000 \\ S(3)=1000(9)+1350-1000 \\ S(3)=9000+1350-1000 \\ S(3)=9350 \end{gathered}`

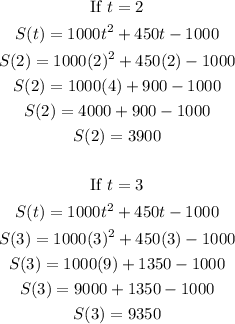
Next, solve for the rate of change over the interval [2,3] using the formula

`\begin{gathered} (\Delta y)/(\Delta t)=(S(3)-S(2))/(3-2) \\ (\Delta y)/(\Delta t)=(9350-3900)/(1) \\ (\Delta y)/(\Delta t)=5450 \end{gathered}`

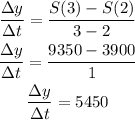
Therefore, the rate of increase of snails from 2 to 3 days is 5450.

Part B: rate of increase from 0 to 2

Using the same formula as above, find the S(0) and S(2)

`\begin{gathered} \text{If }t=0 \\ S(t)=1000t^2+450t-1000 \\ S(0)=1000(0)^2+450(0)-1000 \\ S(0)=-1000 \\ \\ \text{If }t=2 \\ \text{As solved earlier, }S(2)=3900 \end{gathered}`

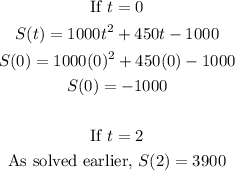
Substituting with a = 0, and b = 2, we have the following

`\begin{gathered} (\Delta y)/(\Delta t)=(S(2)-S(0))/(2-0) \\ (\Delta y)/(\Delta t)=(3900-(-1000))/(2) \\ (\Delta y)/(\Delta t)=(3900+1000)/(2) \\ (\Delta y)/(\Delta t)=(4900)/(2) \\ (\Delta y)/(\Delta t)=2450 \end{gathered}`

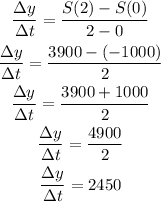
Therefore, the rate of increase of snails after 2 days is 2450.