Question

ariana drew a right triangle, in her right triangle, one of the legs was 17 inches. the other sides she drew had lengths that were consecutive integers find the length of the other leg. how long was the hypothenus that ariana drew, round to the hearst hundreds

Answer 1

Let the longer length of the triangle be

`=x`

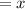
Since they are consecutive integers, The length of the hypotenuse will be

`=x+1`

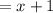
The length of one of the legs is

`=17\text{inches}`

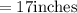
The diagram below represents the right-angled triangle

Concept: To solve this question, we will make use of the Pythagorean theorem

Step 1: State the Pythagorean theorem

`\begin{gathered} \text{hypotenus}^2=\text{opposite}^2+\text{adjacent}^2 \\ \text{where,} \\ \text{Hypotenus}=(x+1)\text{ inches} \\ \text{opposite}=x\text{ inches} \\ \text{adjacent}=17\text{ inches} \end{gathered}`

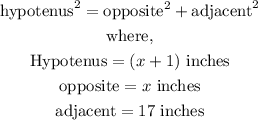
Step 2: Substitute the values in the formula above

`\begin{gathered} \text{hypotenus}^2=\text{opposite}^2+\text{adjacent}^2 \\ (x+1)^2=x^2+17^2 \end{gathered}`

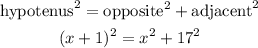
Expand the brackets above, we will have

`\begin{gathered} (x+1)^2=x^2+17^2 \\ (x+1)(x+1)=x^2+289 \\ x(x+1)+1(x+1)=x^2+289 \\ x^2+x+x+1=x^2+289 \\ x^2+2x+1=x^2+289 \end{gathered}`

Collect similar terms, we will have

`\begin{gathered} x^2+2x+1=x^2+289 \\ x^2-x^2+2x=289-1 \\ 2x=288 \\ \end{gathered}`

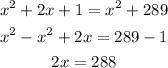
Divide both sides by 2

`\begin{gathered} (2x)/(2)=(288)/(2) \\ x=144 \end{gathered}`

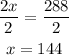
Hence,

The longer leg = 144 inches

The hypotenuse of the triangle was = 145 inches