Step1: write out the equation
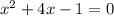
Looking at the equation it cannot be factorized, hence we use the quadratic formula method
Step2: write out the quadratic formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nk3bft20xor7rzbiz28ysgt23i1xfm7d29.png)
where a=coefficient ofx²=1
b=coefficient of x=+4
c= constant =-1
Step3: Substitute the values into the formula above
![x=\frac{-4\pm\sqrt[]{4^2-4(1)(-1)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/t6voe1rt14bs0nssc5l83yk1c9nir8h4on.png)
![\begin{gathered} x=\frac{-4\pm\sqrt[]{16+4}}{2} \\ =\frac{-4\pm\sqrt[]{20}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/svc4y4zqsejcx3ymniurkrv0fgt1kb9bmu.png)
Hence, by splitting the denominator we have
![\begin{gathered} x=(-4)/(2)\pm\frac{\sqrt[]{20}}{2} \\ =-2\pm\frac{\sqrt[]{4*5}}{2} \\ =-2\pm\frac{2\sqrt[]{5}}{2} \\ =-2\pm\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sqc7t7m6tdvv41riwmo2xz9ak8bagaxytg.png)
x=-2±√5
Therefore the right option is c