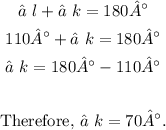Angle m
By Consecutive Interior Angle Theorem, If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary.
In this instance, 130°, and angle m are supplementary
The sum therefore, of their angle is 180°.
![\begin{gathered} 130°+\angle m=180\degree \\ \angle m=180\degree-130\degree \\ \\ \text{Therefore, }\operatorname{\angle}m=50° \end{gathered}]()
Angle n
Since angles m, n and o are angles in a straight line, the sum of their angle is 180°.
Given that angle l is 110° by vertical angle theorem, then angle o = 70°. This means that
![\begin{gathered} \angle m+\operatorname{\angle}n+\operatorname{\angle}o=180\degree \\ 50°+\operatorname{\angle}n+70°=180° \\ 120°+\operatorname{\angle}n=180° \\ \operatorname{\angle}n=180°-120° \\ \\ \text{Therefore, }\angle n=60° \end{gathered}]()
Angle j
By linear pair theorem, 130°, and ∠j are linear pair.
Their sum therefore, is 180°, which means that
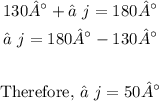
Angle k
Same with above, by linear pair theorem, ∠l and ∠k are linear pair, the sum of their angle is 180° which means that