Step-by-step explanation:
Given;
We are given the equation of a parabola as shown below;
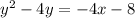
Required;
We are required to find the focus of the parabola.
Step-by-step solution;
We re-write this equation and express x in terms of y;
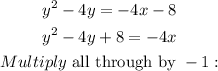
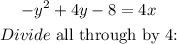
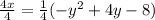
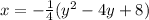
We now write this out in the vertex form which is;
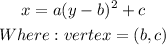
We now simplify the right side of the equation;
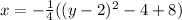
![undefined]()