Question

16. The product of two consecutive negative integers is 10506. Write a quadratic equation that you could solve to find the integers.

Answer 1

Let's call x a negative number. We want the product of x and the one next number to it (x + 1) to be 10506. Then, we can write:

`x(x+1)=10506`

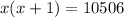
Now, we can apply distributive property on the parentheses, and rest 10506 on both sides:

`x^2+x-10506=0`

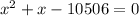
And now, we have a quadratic equation in standard form. We can solve this using the quadratic formula:

`\begin{gathered} x_(1,2)=(-1\pm√(1^2-4\cdot1\cdot(-10506)))/(2\cdot1)=(-1\pm√(42025))/(2)=(-1\pm205)/(2) \\ . \\ x_1=(-1+205)/(2)=(204)/(2)=102 \\ . \\ x_2=(-1-205)/(2)=(-206)/(2)=-103 \end{gathered}`

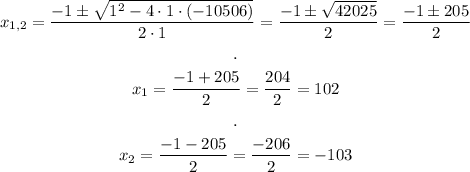
Since we want x to be a negative answer, we take the negative solution, x = -103, And now, we can find the other number:

x + 1 = -103 + 1 = -102

Now, we can verify that the pair of numbers that we have found really are a solution for what we're looking for:

`(-103)(-102)=103\cdot102=10506`

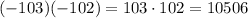
Thus, the equation to solve this is:

`x(x+1)=10506`

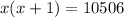
And the solution is:

x = -103

x + 1 = -102