Question

A. (1, -5) B. (0, -4) C. (-3,-1) D. (-5,1) B. (-2, 0) C. (-1,1) D. no solution 9. Consider the system of linear equations shown below. 8x - y = -96 2x + 3y = 12 A. Solve this system using either the substitution or elimination method. Show your work or explain your answer. found in Part A is correct.

Answer 1

`\begin{gathered} x=-6 \\ y=8 \end{gathered}`

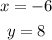
Step-by-step explanation

let

`\begin{gathered} 8x-6y=-96\Rightarrow equation(1) \\ 2x+3y=12\Rightarrow equation(2) \end{gathered}`

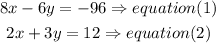
Step 1

A) solve by substitution or elimination

isolate x in equation (2) and then replace in equation (1)

`\begin{gathered} 2x+3y=12\Rightarrow equation(2) \\ \text{subtrac 3y in both sides} \\ 2x+3y-3y=12-3y \\ 2x=12-3y \\ \text{divide both sides by 2} \\ (2x)/(2)=(12)/(2)-(3y)/(2) \\ x=6-(3y)/(2)\Rightarrow equation(3) \end{gathered}`

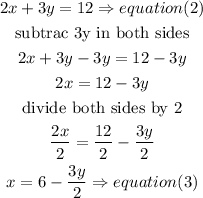
now, replace the x value in equation (1) and isolate y

`\begin{gathered} 8x-6y=-96\Rightarrow equation(1) \\ 8(6-(3y)/(2))-6y=-96 \\ 48-12y-6y=-96 \\ 48-18y=-96 \\ \text{subtract 48 in both sides} \\ 48-18y-48=-96-48 \\ -18y=-144 \\ \text{Divide both sides by -18} \\ (-18y)/(-18)=(-144)/(-18) \\ y=8 \end{gathered}`

finally, replace the y value we just got, in equation (3) to find x

`\begin{gathered} x=6-(3y)/(2)\Rightarrow equation(3) \\ x=6-(3\cdot8)/(2)\Rightarrow equation(3) \\ x=6-(24)/(2) \\ x=6-12 \\ x=-6 \end{gathered}`

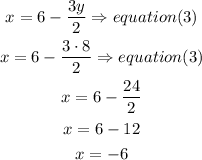
so, the solution of the system of equation is

`(-6,8)`

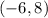
Step 2

briefly describe how you can prove that the solution found in part A is correct:

to prove this we need to replace the values we found, and the equation becomes a true equality

so,

for equation(1)

`\begin{gathered} 8x-6y=-96\Rightarrow equation(1) \\ \text{replace} \\ 8(-6)-6(8)=-96 \\ -48-48=-96 \\ -96=-96\Rightarrow true \end{gathered}`

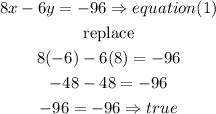
now, equation (2)

`\begin{gathered} 2x+3y=12\Rightarrow equation(2) \\ \text{replace} \\ 2(-6)+3(8)=12\Rightarrow equation(2) \\ -12+24=12 \\ 12=12\Rightarrow true \end{gathered}`

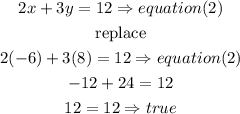
therefore, as we said in the previous part

the solution is

`(-6,8)`

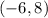
I hope this helps you