Question

I need help solving this practice The instructions are in the photo

Answer 1

To answer this question, we can proceed as follows:

We need to apply the following identity:

`\sin (x+y)=\sin (x)\cos (y)+\cos (x)\sin (y)`

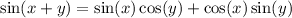
Then we have to find the sine and cosine for the given values. We need to take care of the quadrants for the signs of the functions.

1. We have that:

`\cos \theta=-\frac{\sqrt[]{2}}{3},\pi\leq\theta\leq(3\pi)/(2)`

Therefore, we know that Θ is in the III Quadrant, and we already know that the cosines and sines functions are negative in this quadrant.

Then we have:

To find the opposite side of the triangle - to find later the sine ratio - we can use the Pythagorean Theorem as follows:

`\begin{gathered} (-\sqrt[]{2})^2+x^2=3^2 \\ 2+x^2=9 \\ x^2=9-2 \\ x^2=7 \\ \sqrt[]{x^2}=\sqrt[]{7} \\ x=\sqrt[]{7} \end{gathered}`

Therefore, we have that:

`\sin \theta=-\frac{\sqrt[]{7}}{3}`

We need to remember that the sine function is negative in the III Quadrant.

We have also that:

`\tan \beta=(4)/(3),0\leq\beta\leq(\pi)/(2)`

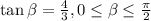
We can see that the values for sine and cosine in the I Quadrant are positive. However, we have the value for tanβ. Therefore, we have:

We have to remember that tan = opposite side / adjacent side. Now, we need to find the hypotenuse to find the sine and cosine for this angle. We can use the Pythagorean Theorem again:

`\begin{gathered} x^2=3^2+4^2 \\ x^2=9+16^{} \\ x^2=25 \\ \sqrt[]{x^2}=\sqrt[]{25} \\ x=5 \end{gathered}`

Therefore, we have:

`\begin{gathered} \sin \beta=(opposite)/(hypotenuse)=(4)/(5)\Rightarrow\sin \beta=(4)/(5) \\ \cos \beta=(adjacent)/(hypotenuse)=(3)/(5)\Rightarrow\cos \beta=(3)/(5) \end{gathered}`

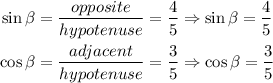
We need to remember that both sine and cosine are positive in the first quadrant.

We know that:

`\sin (x+y)=\sin (x)\cos (y)+\cos (x)\sin (y)`

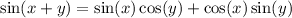
Then

`\sin (\theta+\beta)=\sin (\theta)\cos (\beta)+\cos (\theta)\sin (\beta)`

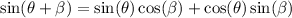
And we got that:

`\begin{gathered} \sin \theta=-\frac{\sqrt[]{7}}{3} \\ \cos \theta=-\frac{\sqrt[]{2}}{3} \\ \sin \beta=(4)/(5) \\ \cos \beta=(3)/(5) \end{gathered}`

Then we have to substitute the corresponding values into the trigonometric identity given above:

`\begin{gathered} \sin (\theta+\beta)=\sin (\theta)\cos (\beta)+\cos (\theta)\sin (\beta) \\ \sin (\theta+\beta)=(-\frac{\sqrt[]{7}}{3})((3)/(5))+(-\frac{\sqrt[]{2}}{3})((4)/(5)) \\ \sin (\theta+\beta)=\frac{-3\sqrt[]{7}}{15}+\frac{-4\sqrt[]{2}}{15} \\ \sin (\theta+\beta)=\frac{-3\sqrt[]{7}-4\sqrt[]{2}}{15} \end{gathered}`

Therefore, we have, in summary, that:

`\sin (\theta+\beta)=\frac{-3\sqrt[]{7}-4\sqrt[]{2}}{15}`

[We can also express the result as follows:

`\begin{gathered} \sin (\theta+\beta)=(-\frac{\sqrt[]{7}}{3})((3)/(5))+(-\frac{\sqrt[]{2}}{3})((4)/(5)) \\ \sin (\theta+\beta)=-\frac{\sqrt[]{7}}{5}-\frac{4\sqrt[]{2}}{15} \end{gathered}`

.]