Question

1. Scheduling Employees: Suppose you own a catering company. You hire temporary employees to act as servers from the local college. Not being the most reliable employees, there is an 80% chance that any one server will actually show up for a scheduled event. For a wedding scheduled on a given Saturday you need at least 5 servers.(a) Suppose you schedule 5 employees, what is the probability that all 5 come to work? (b) Suppose you schedule 7 employees, what is the probability that at least 5 come to work? (c) How many employees should you schedule in order to be 99% confident that at least 5 come to work? Hint: There is no single formula for the answer to this problem, you should use some type of trial and error.

Answer 1

ANSWERS

(a) P(X = 5) = 0.3277

(b) P(X ≥ 5) = 0.8520

(c) 10 employees must be scheduled

Step-by-step explanation

Let X be the number of employees that come to work. X follows a binomial probability with a probability of success p = 0.8.

The probability of exactly x successes on n repeated trials is,

`P(X=x)=_nC_x\cdot p^x(1-p)^(n-x)`

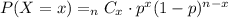
(a) We have to find the probability that exactly 5 out of 5 employees come to work. In this case, n = 5 and x = 5,

`P(X=5)=(5!)/(5!(5-5)!)\cdot0.8^5\cdot0.2^(5-5)=0.8^5\approx0.3277`

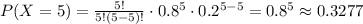
(b) Now, we have to find the probability that of 7 employees, at least 5 come to work. In other words, the probability that 5, 6, or 7 employees come to work,

`P(X\ge5)=P(X=5)+P(X=6)+P(X=7)`

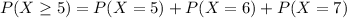
For each of these, n = 7 and x is 5, 6, and 7 respectively,

`P(X\ge5)=(7!)/(5!(5-7)!)\cdot0.8^5\cdot0.2^(7-5)+(7!)/(6!(6-7)!)\cdot0.8^6\cdot0.2^(7-6)+(7!)/(7!(7-7)!)\cdot0.8^7\cdot0.2^(7-7)`

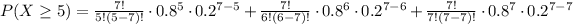
This is,

`P(X\ge5)=0.2752512+0.3670016+0.2097152=0.8520`

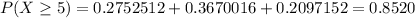
(c) If n is the number of scheduled employees the probability that at least 5 of those will come to work must be at least 99%,

`P(X\ge5)\ge0.99`

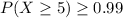
This can be found using trial and error, as stated in the hint. To analyze this we can use the excel command =1 - BINOM.DIST(4, n, 0.8, true) for different values of n. We know from parts a and b that the probability of 5 coming to work when 5 are scheduled is about 32% and when 7 are scheduled to work is about 85%. We have to check values of n greater than 7,

If the probability must be greater than 99%, the minimum number of employees that must be scheduled is 10, and the probability that 5 out of those 10 employees come to work is about 0.9936