Question

In the figure, ABCD and DEFG are squares. AC:FD=7:5, find CE(English isn't my native language. Please correct me if I have any grammatical mistakes.)

Answer 1

Given

The diagonal ratio is given AC:FD=7:5.

The length of AG is 3cm.

Step-by-step explanation

To find CE.

The diagonals ratio is same as the side of square ratio.

Reason-

The diagonals are the square root of 2 multiply by side.

`D=√(2)S`

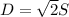
D denotes the diagonal and S denote the side, of suare.

So, the ratio of diagonal is same as the ratio of sides of square.

`(D)/(d)=(S)/(s)`

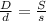
Here D and d denotes the diagonal of the squares and s and S is the sides of squares.

Let AD = 7x , GD = 5x

`\begin{gathered} AG=AD-GD \\ 3=7x-5x \\ 3=2x \\ x=1.5 \end{gathered}`

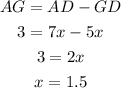
Now find the length of CE,

`\begin{gathered} CE=CD+DE \\ CE=7x+5x \\ CE=12x \end{gathered}`

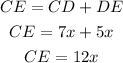
Substitute the value of x in the CE.

`\begin{gathered} CE=12*1.5 \\ CE=18cm \end{gathered}`

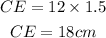
Answer

Hence thelenghth CE is 18cm.