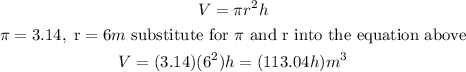Question

There are many cylinders with a radius of 6 meters. Let h represent the height in meters and V represent the volume in cubic meters. a.) Choose an equation that represents the volume Vas a function of the height h. Select] b.) Sketch the graph, using 3.14 as an approximation for it. c.) If you double the height of a cylinder, what happens to the volume? Select ] d.) If you multiply the height of a cylinder by $. what happens to the volume? [Select |

Answer 1

a) Radius of cylinder, r = 6m

where Height is h and Volume is V

`Volume,V=\pi^{}r^2h`

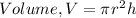
c) if height is doubled

Replace the h with 2h

`h=2(h)=2h`

`V=\pi r^2h^{}`
`V=\pi r^2(2h)`

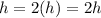
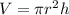
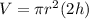
From the equation, the volume will be doubled when the height is doubled.

d) if the height is multiplied by 1/3

Replace h with 1/3(h)

`h=(1)/(3)(h)`
`V=\pi r^2((1)/(3)h)`

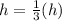
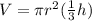
From the equation, the volume of the cylinder will be 1/3 of it's original volume when height is multiplied by 1/3.

b) Where r= 3.14, below lies the graph

`\begin{gathered} V=\pi r^2h \\ \pi=3.14,\text{ r}=6m\text{ substitute for }\pi\text{ and r into the equation above} \\ V=(3.14)(6^2)h=(113.04h)m^3 \end{gathered}`