Question

from my prep guide, I need this question answered, I will provide another picture with the answer options

Answer 1

`(y-k)^2=4p(x-h)`

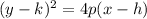
The equation above is the standard form equation of a horizontal parabola and have the next caractheristics:

- The vertex is (h,k)

- If 4p > 0, it opens right

If 4p < 0, it opens left

- | p | is the distance from the vertex to the focus

- The directrix is vertical and the vertex is midway betweeen the focus and directrix

- The directrix is 2| p | units from the focus

For the given parabola:

`\begin{gathered} (y+1)^2=12(x-3) \\ \\ k=-1 \\ h=3 \\ 4p=12 \\ p=(12)/(4)=3 \end{gathered}`

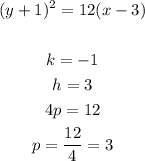
Focus coordinates: It has the same y-coordinate that the vertex, the x-coorcdinate is |p| units to the right (as the parabola opens right) from the x-coordinate of the vertex:

`\begin{gathered} \text{focus: } \\ (h+\lvert p\rvert,k) \\ \\ (3+3,-) \\ (6,-1) \end{gathered}`

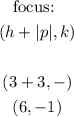
Directrix: it is a vertical line as follow (for a parabola that opens right)

`\begin{gathered} \text{Directrix:} \\ x=h-\lvert p\rvert \\ \\ x=3-3 \\ x=0 \end{gathered}`

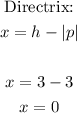
The vertex of the parabola is (3, -1). The parabola opens right, and the focus is 3 units away from the vertex. The directrix is 6 units from the focus. The focus is the point (6, -1). The directrix of the equation is x=0