Answer:
(-2, 2) & (-4, -4)
Step-by-step explanation:
We are given the graph of the equation 6x + 2y = -8
We are to check if the following points are a solution to the inequality 6x + 2y ≤ -8
We will do this using 2 methods:
I. Substitution method
II. Graphical method
I. For the substitution method, we will substitute the variables into the inequality as shown below:
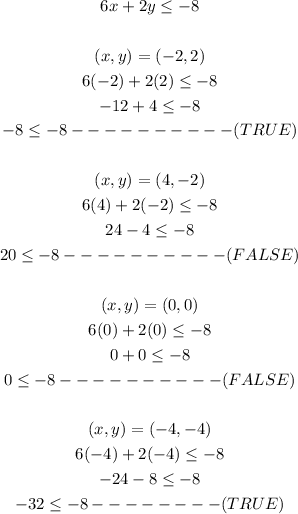
II. For the graphical method, we have:
The solution is given by any point that falls within the shaded portion of the graph
Therefore, the points (-2, 2) & (-4, -4) is a solution to the inequality 6x + 2y ≤ -8