Question

I will show you the pic

Answer 1

The given system of equation :

2x + y = 7 (1)

3x -4y = 5 (2)

Substitution Method :

The substition method involves various steps:

In the system of two equations with two unknown values, the solution can be obtained by using the below steps. Here, the list of steps is provided to solve the linear equation. They are

0. Simplify the given equation by expanding the parenthesis

,

1. Solve one of the equations for either x or y

,

2. Substitute the step 2 solution in the other equation

,

3. Now solve the new equation obtained using elementary arithmetic operations

,

4. Finally, solve the equation to find the value of the second variable

Step 1 : Simplify the given equation by expanding the parenthesis

`\begin{gathered} 2x\text{ + y = 7} \\ 3x\text{ -4y =5} \end{gathered}`

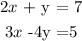
Step 2 : Solve one of the equations for either x or y

Solve the equation (1) for y

`\begin{gathered} 2x+y=7 \\ y=7-2x \end{gathered}`

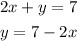
Step 3 : Substitute the step 2 solution in the other equation

Substitute the value of y = 7 -2x in the equation (2)

`\begin{gathered} 3x-4y\text{ = 5} \\ 3x-4(7-2x)=5 \\ 3x-28+8x=5 \end{gathered}`

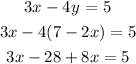
Step 4 : Now solve the new equation obtained using elementary arithmetic operations

`\begin{gathered} 3x-28+8x=5 \\ 11x-28=5 \\ 11x=28+5 \\ 11x=33 \\ x=(33)/(11) \\ x=3 \end{gathered}`

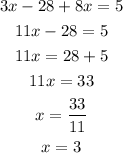
Step 5: Finally, solve the equation to find the value of the second variable

Substitute the value of x = 3 in the equation(1)

`\begin{gathered} 2x+y=7 \\ 2(3)+y=7 \\ 6+y=7 \\ y=7-6 \\ y=1 \end{gathered}`

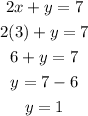
y=1

The solution of the system of equations are : (x,y) = (3,1)

Answer : D) (3,1)