Question

Identify the polynomial that is not the difference of two squares. a. 80/6 - 9y4b. 16x2 - 625 c. 476 - 9y6 d. 169x2 - 4y4

Answer 1

At first , we should know that:

The polynomial that is a difference between two squares can be factored to :

`(x-a)\cdot(x+a)=x^2-a^2`

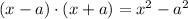
So, both of x^2 and a^2 is a complete square

So, we will check the options :

A. 80/6 - 9y4

80/6 is not a complete square but 9y^4 is a complete square

9y^4 = 3y^2 * 3y^2

B. 16x^2 - 625

Both of 16x^2 and 625 is complete square

16x^2 = 4x * 4x

625 = 25 * 25

C. 476 - 9y^6

476 is not a complete square but 9y^6 is a complete square

D. 169x^2-4y^4

Both of them is a complete square

169x^2 = 13x * 13x

4y^4 = 2y^2 * 2y^2

so, the answer is the options A and C