Question 5
Two angles are called complementary if their measures add to 90 degrees.
Given:
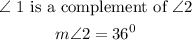
Applying the definition for complementary angles, we can write:
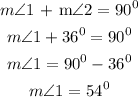
Answer: 54 degrees
Question 6
Given:
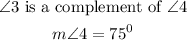
Applying the definition for complementary angles, we can write:
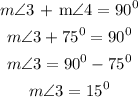
Answer: 15 degrees
Question 7
Two angles are called supplementary if their measures add to 180 degrees.
Given:
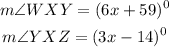
Using the definition for supplementary angles, we can write:
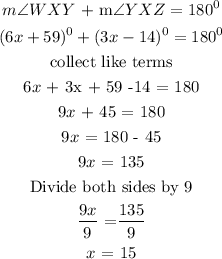
Substituting the value of x into angles WXY and YXZ:
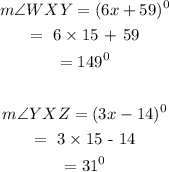
Answer:
The measure of angle WXY = 149 degrees
The measure of angle YXZ = 31 degrees