Question

If you drop a 2.2 kg ball from the top of a 39 m high, how fast will it be going when it’s still 17 m above the ground? Round your answer to the nearest tenth and include the appropriate unit.

Answer 1

We are given that a ball is dropped from a height of 39 meters and we are asked to determine the velocity of the ball when it is 17 meters above the ground. To do that we will use the conservation of energy.

The energy when the ball is dropped is the gravitational potential energy and is given by the following formula:

`E_1=mgh_0`

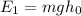
Where:

`\begin{gathered} E_1=\text{ initial energy} \\ m=\text{ mass} \\ g=\text{ acceleration of gravity} \\ h_0=\text{ initial height} \end{gathered}`

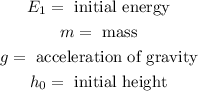
Now, when the ball is 17 meters above the ground part of the gravitational potential energy has converted into kinetic energy. The kinetic energy is given by the following formula:

`K=(1)/(2)mv^2`

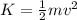
Where:

`v=\text{ velocity}`

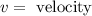
Therefore, at the second point the ball has kinetic energy and gravitation al potential energy:

`E_2=(1)/(2)mv^2+mgh_2`

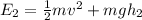
Using conservation of energy we can set both energies equal:

`mgh_0=(1)/(2)mv^2+mgh_2`

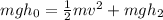
Now, we can solve for the velocity. To do that we will first cancel out the mass "m":

`gh_0=(1)/(2)v^2+gh`

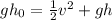
Now, we subtract "gh2" from both sides:

`gh_0-gh_2=(1)/(2)v^2`

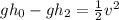
Now, we multiply both sides by 2:

`2(gh_0-gh_2)=v^2`

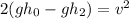
Now, we can take "g" as a common factor:

`2g(h_0-h_2)=v^2`

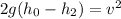
Now, we take the square root to both sides:

`√(2g(h_0-h_2))=v`

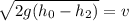
Now, we substitute the values:

`\sqrt{2(9.8(m)/(s^2))(39m-17m)}=v`

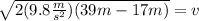
Now, we solve the operations:

`20.8\text{ m/s=}v`

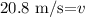
Therefore, the velocity of the ball is 20.77 m/s.