Answer:
C. 25
Step-by-step explanation:
Let the number of hours Jack can work = x
Let the number of hours Jane can work = y
If they do not want to work over 65 hours per week combined, then:
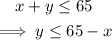
Jack is paid $10 per hour at his.
Jane is paid $12.50 per hour at her job.
They need to make a minimum of $750 per week.
Therefore:
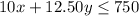
To make it easier, we solve the system of equations below.

Therefore, the maximum amount of hours that Jack can work per week according to these limits is 25 weeks.