Answer:
The equation is given below as
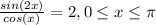
Step 1:
Cross multiply
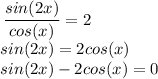
Step 2:
Apply the trig identity below


Step 3:
Factor out 2cos(x)
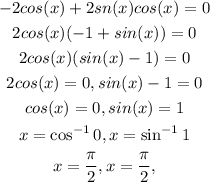
Step 4:
Check for undefined points
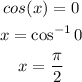
Since the equation is undefined for π/2,
Hence,
There is no solution for x
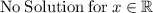
Her error is that π/2 will make the equation undefined for the equation in the question.
Therefore,
π/2 cannot be the answer