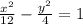Question

Which is the equation of a hyperbola with directrices at x = ±3 and foci at (4, 0) and (−4, 0)?​

Answer 1

`(x^2)/(12)-(y^2)/(4)=1`

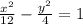
Explanation:

Since our foci are located on the x-axis, then our major axis is going to be the horizontal transverse axis of the hyperbola:

Formula for hyperbola with horizontal transverse axis centered at origin

• 
  `(x^2)/(a^2)-(y^2)/(b^2)=1`
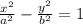
• Directrices ->
  `x=\pm(a^2)/(c)`
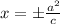
• Foci ->
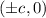  `(\pm c,0)` where
  `a^2+b^2=c^2`
• 
  `a>b`

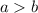
Since we are given our directrices of
`x=\pm3` and foci of
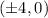`(\pm4,0)`, then we can set up the directrices equation to solve for
`a^2`:

`x=\pm(a^2)/(c)\\ \\\pm3=\pm(a^2)/(4)\\ \\12=a^2`

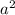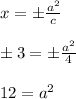
Now we can determine
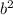`b^2` to complete our equation for the hyperbola:

`a^2+b^2=c^2\\\\12+b^2=4^2\\\\12+b^2=16\\\\b^2=4`

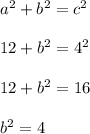
Therefore, our equation for our hyperbola is
`(x^2)/(12)-(y^2)/(4)=1`