$46305
Step-by-step explanation:
First year pay = $40000
Rate of Increase = 5% per year after the first year
Second year pay = 40000(1.05)
To get the formula for subsequent years, we will use an exponential growth formula:
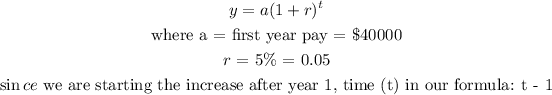
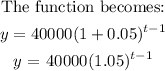
in the fourth year: t = 4

You are expected to earn $46305 in your fourth year on the job