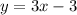The equation of a line in the slope-intercept form is y = mx + b.
Given the points (-4, -15) and (5, 12), follow the steps below to find the equation of the line.
Step 01: Substitute the first point in the equation.
Given the point (-4, -15)
Then, when x = -4, y = -15
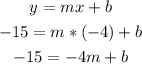
Add 4m to both sides to solve for b:
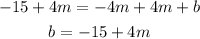
Step 02: Substitute b in the equation.
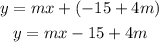
Step 03: Substitute the second point in the equation.
Given the point (5, 12).
Then, when x = 5, y = 12
Substituting it in the equation:
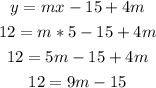
Adding 15 to both sides and then dividing the sides by 9:
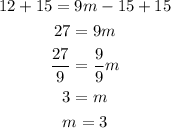
Step 04: Find b and substitute b and m in the equation.
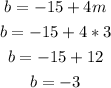
The equation of the line is:
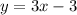
Answer: