
As the vertex is (h,k)
And in the given graph you have the vertex in (24,50)
You have the next:
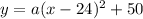
You use this equation and the value of x and y in the graph (example: (44,0)) to find the coefficient a:

Solve the operation to remove parenthesis:
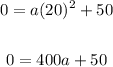
Substract 50 in both sides of the equation:
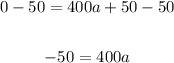
Divide both sides of the equation into 400:
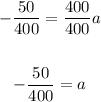
Simplifty:
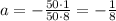
Then, the value of coefficient a is -1/8